Pythonで数学を学ぼう：円周率を求める

問題編

基本的な方策

円の面積を求めれば円周率がわかります。 円の面積をS、半径をrとすると、

$$\begin{equation} S = \pi r^2 \end{equation}$$

なので、もし半径が1なら

$$\begin{equation} S = \pi \end{equation}$$

となるのです。このように、円の面積を求めると円周率がすぐわかります。 今回は、Pythonを使って、いかにもコンピューターっぽく、「小さい計算をたくさん繰り返す」やりかたで円の面積を求めてみることにしましょう。

復習：なぜ $S = \pi r^2$ なのか？

(1) モンテカルロ法で円の面積を求めよう

モンテカルロ法：ランダムな試行を繰り返すことで値を求めるやりかた

この四角の中にランダムで点をたくさん打ったとき、円の中に入った点の割合から円の面積を求めることができる。

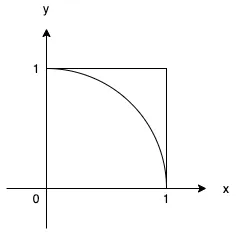
具体的には、このように円の1/4を切り出して、xが0から1まで、yが0から1までの間の数値をランダムでとるときに、円の中に入る数を求める。このとき、ピタゴラスの定理により、以下の場合に円の中に入ることになる。

$$\begin{equation} x^2 + y^2 < 1 \end{equation}$$

Pythonで0から1までの間の乱数を求める方法

from random import random
x  = random()

(2) 積分で円の面積を求めよう

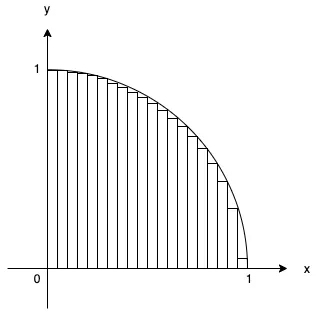
円の中に小さい長方形を敷き詰めます。長方形の面積を足すと円の面積に近いものになります。このとき、長方形を細くすれば細くするほど円の面積に近づきます。

xとyの関係は、

$$\begin{equation} x^2 + y^2 = 1 \end{equation}$$

なので、xの地点の長方形の高さyは

$$\begin{equation} y = \sqrt{1 - x^2} \end{equation}$$

で求められます。これをPythonで表すと、

import math
y = math.sqrt(1 - x**2)

となります。

解答編

復習：なぜ $S = PIr^2$ なのか？ → 円を限りなく細かい扇形に分割して、互い違いに組み合わせて長方形を作ると、長辺 r 、短辺 r となるから。

(1) モンテカルロ法で円の面積を求めよう

from random import random
total = 1000000
ok = 0
for i in range(total):
    x = random()
    y = random()
    if 1 > x*x + y*y:
        ok += 1
print(ok/total*4)

(2) 積分で円の面積を求めよう

import math
total = 10000000
size = 0
for n in range(total):
    x = n/total
    y = math.sqrt(1 - x*x)
    size += y*(1/total)
print(size*4)