ライブラリ:Numpy入門(数値計算)
Numpy(ナムパイ)はPythonの数値計算用のライブラリで、大規模な多次元配列や行列の計算が得意です。(※注) Numpyは、今後さらに注目されてくる データサイエンス や 機械学習 、および 量子プログララミング の分野で頻繁に使われますので、見慣れておくと良いでしょう。また、画像処理ライブラリのPillowなどと組み合わせることで、 画像データを加工 して減色処理やガンマ補正などを行うことができます。
行列計算の身近な応用例としては、連立方程式を解く などがあります。(学校の宿題には使わないように!!)
※注:Pythonには、Numpyよりもさらに高度な科学技術計算をおこなうことが可能なライブラリSciPy(サイパイ)などもあります。SciPyでは微積分や統計で使われる標準偏差などの計算もできます。
1. 準備
インポート:import
Numpyを使って多次元配列の計算をするには、ライブラリをインポートします。
import numpy as np(参考)
-
ベクトル、行列、配列、多次元配列
Numpyでは、ベクトル、行列、配列、多次元配列といった言葉が出てきます。学校の数学でもベクトルや行列などを学ぶので混乱するかもしれませんが、最初のうちは数学の世界とプログラミングの世界とは別だと考えた方が良いでしょう。ざっくり言うと、プログラミングの世界では、ベクトルも行列も配列の一種です。シンプルに、 1次元の配列 を ベクトル 、 2次元の配列 を 行列 とも言うと思っていいでしょう。そして 多次元配列 とは一般的に2次元以上の配列を言い、 n次元配列 という言い方もします。(3次元以上の多次元配列のことをテンソルと呼ぶこともあります) ここは入門編なので、1次元配列(ベクトル)か2次元配列(行列)での説明にしています。より多次元の配列で後述のメソッドや関数を使うこともできますが、説明が複雑になるので割愛しています。
-
ndarray
Numpyでは、 ndarray という言葉もしばしば出てきます。ndarrayはN dimension array(n次元配列)の略で、「エヌ・ディー・アレイ」と読みます。ndarrayはNumpyで使う配列のデータ型(正確にはpythonのクラス)の名前です。np.array()で作った配列をtype()で型を調べると、<class ‘numpy.ndarray’>と表示されます。 注:Numpyには ndarray型 と同じような matrix型 というのもありますが、matrix型は非推奨なので、ここでは扱いません。
-
Python標準の配列(リスト)とNumpyの配列の違いと見分け方
Pythonは標準で(importとかなしに)配列(リスト)を使うことができます。しかしこれは、Numpyの配列とは別のものです。 まず、型(クラス)が別のものです。Python標準の配列(リスト)は listクラス 、Numpyの配列は numpy.ndarrayクラス になります。クラスが違うので、使えるメソッドも異なり(Numpy配列の方が多種・高機能です)、格納できる要素の条件も違いがあります。 また、printでの表示も異なり、 Numpy配列ではカンマ(,)がありません ので、見分けることができます。
import numpy as np
#Python標準の配列(リスト)p = [0, 1, 2]print(p)# [0, 1, 2] 要素の区切りにカンマ(,)がある
print(type(p))# <class 'list'>
#Numpyの配列v = np.array([0, 1, 2])print(v)# [0 1 2] 要素の区切りにカンマ(,)がない
print(type(v))# <class 'numpy.ndarray'>2. 配列を作る
配列を作る:np.array()
1次元配列(ベクトル)
import numpy as np
v = np.array([0, 1, 2, 3, 4])print(v)# [0 1 2 3 4]2次元配列(行列)
import numpy as np
m = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])print(m)# [[0 1 2]# [3 4 5]# [6 7 8]]やってみよう1
自分で好きな大きさの配列を作ってみよう。2行5列とかも作ってみよう。また、要素を整数ではなく、実数(小数付きの数字)や文字列などにしてみよう。どのように表示されるでしょうか。
※Numpyの配列(ndarrayオブジェクト)は、基本的にはすべての要素が同じデータ型(整数型とか実数型とか)となります。一つのNumpy配列で複数のデータ型を扱うためのStructured Data(構造化データ)という仕組みもありますが、ここでは触れません。
要素がゼロの配列を作る:np.zeros()
1次元配列(ベクトル)
import numpy as np
v = np.zeros(5) #引数に配列のサイズを指定print(v)# [0. 0. 0. 0. 0.] # 0.は 0.0の省略形2次元配列(行列)
import numpy as np
m = np.zeros((2, 3)) #引数に配列の形態を指定print(m)# [[0. 0. 0.]# [0. 0. 0.]]連番の配列を作る:np.arange()
1次元配列(ベクトル)
import numpy as np
v = np.arange(0,5) #0から4までの連続値print(v)# [0 1 2 3 4]
v = np.arange(5) #最初の"0,"は省略できるprint(v)# [0 1 2 3 4]2次元配列(行列)
import numpy as np
m = np.arange(6).reshape(2,3) #np.arange()で連番の1次元配列を作り、.reshape()で2次元配列に変形するprint(m)# [[0 1 2]# [3 4 5]]空の配列を作る:np.empty()
注1)np.empty()では領域確保だけ行い、要素の値の初期化は行いません。
注2)配列の値の型は、デフォルトだと実数( float64 )になります。第二引数 dtype で指定することもできます。
1次元配列(ベクトル)
import numpy as np
# 配列の大きさを指定して作成v=np.empty(5)print(v)# [0.000e+000 0.000e+000 0.000e+000 3.577e-321 0.000e+000] 初期化を行わないので、不定な値となる
# 配列の大きさと型を指定して作成v=np.empty(5, dtype=np.int64) # 型を整数(int64)と指定するfor i in range(5): v[i]= input() # 添字で指定して代入ができる。この例ではコンソールから0~5を手入力。print(v)# 0# 1# 2# 3# 4# [0 1 2 3 4]
# 要素が全く無い配列を作成v = np.empty(0)print(v)# [] 要素が全くないので、代入するには関数append()で追加していく必要がある。2次元配列(行列)
import numpy as np
m=np.empty((2,3))print(m)# [[ 0.00000000e+000 0.00000000e+000 4.28848981e-321] 初期化を行わないので、不定な値となる# [ 0.00000000e+000 -1.08711402e-311 0.00000000e+000]]空の2次元配列への代入例(この行をクリックすると表示されます)
import numpy as np
m=np.empty((2,3), dtype=np.int64) # 型を整数(int64)と指定するfor i in range(2): for j in range(3): m[i,j]= input() # コンソールから手入力。下記の例では0~5を入力print(m)# 0# 1# 2# 3# 4# 5# [[0 1 2]# [3 4 5]]※この他にも、乱数の配列を作る(np.random.rand())、単位行列を作る(np.eye())などもありますので、興味のある方は調べてみてください。
3. 配列の要素を参照をする
インデックス(添字)による要素の指定:[ ]
注:添字は0始まり
1次元配列(ベクトル)
import numpy as np
v = np.array([0, 1, 2, 3, 4])print(v)# [0 1 2 3 4]
print(v[3]) #第3番(前から4つ目)の値を表示# 3
print(v[-1]) #最後の値を表示# 42次元配列(行列)
import numpy as np
m = np.arange(9).reshape(3,3)print(m)# [[0 1 2]# [3 4 5]# [6 7 8]]
print(m[1,2]) #第1行の第2列の値を表示# 5
print(m[-1,1]) #最後の行(この場合は第2行)の第1列の値を表示# 7
print(m[1]) #第1行を表示# [3 4 5]※要素の指定は原則、下記のようになります。
Python標準のリストの場合、 p[行][列] の形で指定する。(p[行,列]はエラー) Numpy の配列の場合、 m[行,列] の形で指定する。 (m[行][列]でも可)
スライス操作による取り出し:[start : stop : step]
Pythonではコロン(:)を使って表すスライス(例 [2 : 4])によって、リストや配列などの一部分を選択して取得したり別の値を代入したりできます。 スライスでは選択範囲の開始位置(インデックス)と終了位置(インデックス)、ステップを [開始位置 : 終了位置 : ステップ] のように書くと、開始位置 以上 、終了位置 未満 の要素が、ステップで示した間隔で取り出されます。
開始・終了位置は配列の添字と同様、 0始まり になっています。 ステップとその直前の ”:” は省略可(例 [2 : 4])で、省略時のステップは1です。 開始位置が書かれていない場合(例 [ : 4])は最初から、終了位置が書かれていない場合(例 [2 :])は最後まで、となります。 開始位置や終了位置がマイナスの値だと、最後尾から数えることになります。 最後尾は-1です。ステップがマイナスだと、逆順に取り出していくことになります。
1次元配列(ベクトル)
import numpy as np
v = np.array([0, 1, 2, 3, 4, 5])print(v)# [0 1 2 3 4 5]
print(v[2:4]) #第2番以上第4番未満。ステップは省略なので、1。(以下同様)# [2 3]
print(v[:3]) #最初から第3番未満まで# [0 1 2]
print(v[3:]) #第3番から最後まで# [3 4 5]
print(v[-1:]) #最後尾のみ# [5]
print(v[:-1]) #最後尾を除いたもの# [0 1 2 3 4]
print(v[1:4:2]) #第2番以上第4番未満をステップ2で# [1 3]
print(v[4:2:-1]) #第4番から第2番未満までを逆順に# [4 3]
print(v[::-1]) #全ての要素を反転# [5 4 3 2 1 0]2次元配列(行列)
import numpy as np
m = np.arange(16).reshape(4,4)print(m)# [[ 0 1 2 3]# [ 4 5 6 7]# [ 8 9 10 11]# [12 13 14 15]]
print(m[1:3,1:3]) #第1行以上第3行未満と、第1列以上第3列未満を表示# [[ 5 6]# [ 9 10]]
print(m[:,2]) #全行の第2列を表示(:のみは全てを意味する)# [ 2 6 10 14]4. 配列のメソッドを使う
以下の例では1次元配列で示しています。多次元配列の場合は1次元配列に直してから同様に計算されます。
import numpy as np
v = np.array([0, 1, 2, 3, 4])print(v)# [0 1 2 3 4]※以下、上記配列 v に対するメソッドを示します。
最大値: .max()
print(v.max())# 4最小値:.min()
print(v.min())# 0合計:.sum()
print(v.sum())# 10平均値:.mean()
print(v.mean())# 2.0(参考)
分散:.var()
print(v.var())# 2.0標準偏差:.std()
print(v.std())# 1.41421356237309515. 配列の情報を確認する
ndarrayクラスの配列は、その属性(プロパティ、フィールド)として、様々な情報を持っています。
import numpy as np
v = np.array([0, 1, 2, 3, 4])m = np.array([[0, 1, 2], [3, 4, 5]])
print(v)# [0 1 2 3 4]print(m)# [[0 1 2]# [3 4 5]]※以下、上記配列 v, m に対する属性を示します。
次元:.ndim
配列の次元を表します。最初の ”[” の数に対応します。
print(v.ndim)# 1 1次元print(m.ndim)# 2 2次元形状:.shape
配列の行数・列数を表します。
print(v.shape)# (5,) 5列print(m.shape)# (2, 3) 2行3列※1次元配列(ベクトル)の形状の表示が奇妙に感じるかもしれませんが、こういうもんだと思って覚えてください。
サイズ:.size
行列の要素の全個数です。
print(v.size)# 5 5個print(m.size)# 6 6個データ型:.dtype
要素のデータ型を表します。(基本的には一つの ndarray オブジェクトに対して一つの dtype が設定されていて、すべての要素が同じデータ型となります。)
print(v.dtype)# int32 符号あり32ビット整数型print(m.dtype)# int32 符号あり32ビット整数型6. 配列を操作する
メソッド(例 v.reshape(2,3))もしくは関数(例 np.flip(v))などによって、配列を変形することができます。
注)正確に言うと、操作によって 元の配列が書き換えられる場合 と単に変形した 結果が表示されるだけの場合 とで違いがありますが、ここでは入門編なので、同じように結果が表示されるならば同じものとして示しています。
import numpy as np
v = np.array([0, 1, 2, 3, 4, 5])print(v)# [0 1 2 3 4 5]※以下、上記配列 v を順次操作した例を示します。
配列すべての要素に対して計算する:
m1 = v * 2 #print(m1)# [ 0 2 4 6 8 10]
m2 = v / 2 #print(m2)# [0. 0.5 1. 1.5 2. 2.5]1次元配列を2次元配列に変形する:.reshape()
m = v.reshape(2,3) #2行3列の2次元配列に変形するprint(m)# [[0 1 2]# [3 4 5]]多次元配列を1次元配列にする:.flatten()
vm = m.flatten()print(vm)# [0 1 2 3 4 5]配列の要素を反転する:np.flip(), [::-1]
print(np.flip(v))print(v[::-1])
# どの方式でも同じ表示になる# [5 4 3 2 1 0]配列の要素を並べ替える:np.sort(), .sort()
rand_v = np.array([3, 1, 5, 4, 0, 2])print(rand_v)# [3 1 5 4 0 2]
# sort**関数**でソート・・・元の配列を書き換えないprint(np.sort(rand_v))# [0 1 2 3 4 5] sort関数はソート結果を返すprint(rand_v)# [3 1 5 4 0 2] sort関数は元の配列を書き換えない
# sort**メソッド**でソート・・・元の配列を書き換えるprint(rand_v.sort())# None sortメソッドは値を返さない(None)が、ソートは実行されているprint(rand_v)# [0 1 2 3 4 5] sortメソッドは元の配列を書き換える配列に要素を加える:np.append()
app_v = np.append(v,10)print(app_v)#[ 0 1 2 3 4 5 10]注)上記のvなど、Numpyで生成した配列(ndarray)には appendメソッドはありません 。Python標準のリストと混同しないようにしましょう。
注)配列から要素を削除するには np.delete() 関数がありますが、指定のしかたが複雑なので、ここでは省略します。
注)多次元配列の反転や並べ替えや要素の追加は複雑になるのでここでは省略しますが、興味のある人はネット等で調べてみてください。
以下の操作は入門編としては難しい内容ですが、実際のデータサイエンスや機械学習では頻繁に使われます。
転置行列:.T, .transpose(), np.transpose()
行と列を入れ替えます
import numpy as np
m = np.array([[0, 1, 2], [3, 4, 5]])print(m)# [[0 1 2]# [3 4 5]]
print(m.T)print(m.transpose())print(np.transpose(m))
# どの方式でも同じ表示になる# [[0 3]# [1 4]# [2 5]]逆行列:np.linalg.inv()
import numpy as np
m = np.array([[0, 1], [2, 3]])print(m)# [[0 1]# [2 3]]
print(np.linalg.inv(m))# [[-1.5 0.5]# [ 1. 0. ]]行列式:np.linalg.det()
import numpy as np
m = np.array([[0, 1], [2, 3]])print(m)# [[0 1]# [2 3]]
print(np.linalg.det(m))# -2.0固有値・固有ベクトル: np.linalg.eig()
固有値・固有ベクトルは、様々なところで使われます。例えば、データサイエンスや統計学で主成分分析をする場合に用いられます。また、量子力学の方程式や数学・物理学の理論などにも使われています。興味のある方は調べてみてください。
import numpy as np
m = np.array([[8, 1], [4, 5]])print(m)# [[8 1]# [4 5]]
print(np.linalg.eig(m))# (array([9., 4.]), array([[ 0.70710678, -0.24253563],# [ 0.70710678, 0.9701425 ]]))行列mにおいて、
固有値「9.0」の時の固有ベクトルは( 0.70710678 0.70710678)の定数倍で、(1 1)など 固有値「4.0」の時の固有ベクトルは(-0.24253563 0.9701425)の定数倍で、(-1 4)など
7. 配列同士で演算をする
同じ値を見つける:np.intersect1d()
※多次元配列の場合は、自動的に1次元配列に直して計算されます。
import numpy as np
v1 = np.array([5, 4, 3, 2, 1, 0])v2 = np.array([5, 9, 7, 3, 8, 0, 1])print(v1)# [5 4 3 2 1 0]print(v2)# [5 9 7 3 8 0 1]
print(np.intersect1d(v1, v2))# [0 1 3 5]四則演算
行列の足し算、引き算、掛け算、割り算です。掛け算以外はどれも同じ位置の要素同士の演算になります。なお、それぞれの配列の形状や次元が異なると下記と同様の結果にはならない場合もありますので、注意してください。
import numpy as np
m1 = np.array([[1, 2], [3, 4]])m2 = np.array([[2, 4], [6, 8]])
print(m1)# [[1 2]# [3 4]]
print(m2)# [[2 4]# [6 8]]※以下、上記配列 m1, m2 の演算を示します
足し算:+, np.add()
同じ位置の要素同士の和です
print(m1+m2)print(np.add(m1, m2))
# どの方式でも同じ表示になる# [[ 3 6]# [ 9 12]]引き算:-, np.subtract()
同じ位置の要素同士の差です
print(m1-m2)print(np.subtract(m1, m2))
# どの方式でも同じ表示になる# [[-1 -2]# [-3 -4]]掛け算
(1) 行列積:np.dot(), dot(), @, np.matmul()
数学でよく使われる、通常の行列の積です。機械学習の分野では、しばしばパラメータの更新などに使用されます。
print(np.dot(m1, m2))print(m1.dot(m2))print(m1@m2)print(np.matmul(m1, m2))
# どの方式でも同じ表示になる# [[14 20]# [30 44]]x = np.array([1,2])
print(np.dot(m1, x))print(m1.dot(x))print(m1@x)print(np.matmul(m1, x))
# どの方式でも同じ表示になる# [ 5 11](2) アダマール積:*, np.multiply()
同じ位置の要素同士の積です。
print(m1*m2)print(np.multiply(m1, m2))
# どの方式でも同じ表示になる# [[ 2 8]# [18 32]](3) 行列の内積:
アダマール積の和です
print(np.sum(m1*m2))# 60割り算:/, np.divide()
同じ位置の要素同士の除算です
print(m1/m2)print(np.divide(m1, m2))
# どの方式でも同じ表示になる# [[0.5 0.5]# [0.5 0.5]]8.応用分野
(1)連立一次方程式を解く:np.linalg.solve()
Numpyを使えば、連立方程式を解くこともできます。
例
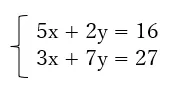
import numpy as np
A = np.array([[5, 2], [3, 7]])b = np.array([16, 27])
print(np.linalg.solve(A, b))#[2. 3.]これにより、x=2.0, y=3.0 が求まります。
(2)偏差値を求める:
Numpyを使えば、得点のリストからそれぞれの偏差値を求めることができます。
例
# 注).round(1)は、数値を小数点以下1桁に丸めるメソッド
import numpy as npimport math
tokuten = [45,63,43,87,53,74,84,55,69,64];np_tokuten = np.array(tokuten)print("得点 :",np_tokuten)
heikin = np_tokuten.mean().round(1)print("平均 :",heikin)
np_hensa = np_tokuten - heikinprint("偏差 :",np_hensa)
bunsan = np_tokuten.var().round(1)print("分散 :",bunsan)
hyoujun_hensa = np_tokuten.std().round(1)print("標準偏差:",hyoujun_hensa)
np_hensachi = ((np_hensa/hyoujun_hensa)*10 + 50).round(1)print("偏差値 :",np_hensachi)
# 得点 : [45 63 43 87 53 74 84 55 69 64]# 平均 : 63.7# 偏差 : [-18.7 -0.7 -20.7 23.3 -10.7 10.3 20.3 -8.7 5.3 0.3]# 分散 : 205.8# 標準偏差: 14.3# 偏差値 : [36.9 49.5 35.5 66.3 42.5 57.2 64.2 43.9 53.7 50.2](3)画像ファイルをnumpy配列のデータに変換する:
機械学習においては、画像ファイル(.jpgや.pngなど)のデータそのままでは処理できませんので、numpyの配列(ndarray)に変換する必要があります。
なお、numpyには画像ファイルを読み込む機能が無いので、まずはPiiowライブラリやOpenCVライブラリを使って画像ファイルを読み込みます(以下の例では、Pillowを使っています)。それをnp.array()に渡します。すると、形状shapeが(行(高さ), 列(幅), 色(チャンネル))の三次元の配列ndarrayが得られます。
例
import numpy as npimport matplotlib.pyplot as pltfrom PIL import Image
image = Image.open("test.jpg")image_array = np.array(image)print(image_array.shape)print(image_array)
plt.imshow(image_array)plt.show()結果
(427, 640, 3) #高さ427×幅640の画像で、R,G,Bそれぞれのチャンネルの明度のデータがある[[[138 141 130] [138 141 130] [142 142 130]...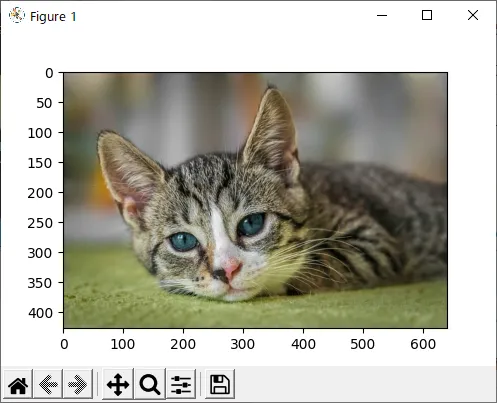
9. スキルアップ
Numpyをマスターするには、Numpy100本ノックなどがあります。原本は英語ですが、ネット上には日本語での解説がたくさんありますので、検索してみてください。
