コンテンツにスキップ
プログラミング教材

１１．当たり判定をしよう

[未完箇所]

  • 冒頭と4章での「ボールキャッチでの当たり判定」のリンク

当たり判定とは、マウス、円や四角などウィンドウ上のモノ同士がぶつかった状態（重なった状態）であるかどうかを調べる（判定する）ことをいいます。ゲームなどでは必須のプログラミングです。

１．マウスと円の当たり判定

※円は正円に限ります

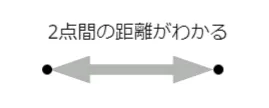
円形の当たり判定は難しそうですが、点と点の間の距離を測る命令 dist( ) を使うと簡単にできます。

dist( ) は、2点の座標を引数で渡すと、2点間の距離を戻り値として渡してくれます。戻り値はfloat型となります。

float d = dist(x1,y1,x2,y2);

ellipse(x,y,200,200); と書くと、円の中心は x,y の座標、半径は直径の半分なので100（=200÷2）となりますね。

座標 x,y を中心に100以内の範囲は、円の中とも考えられます。

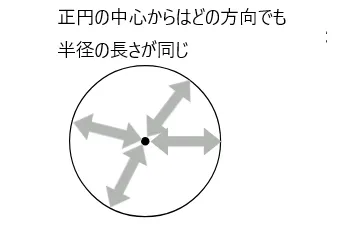
そこで、円の中心とマウスの座標の間の距離と円の半径の長さをくらべて、もし円の中心からマウスまでの距離が、円の半径より短かければ、マウスの座標は円の中にあると考えます。

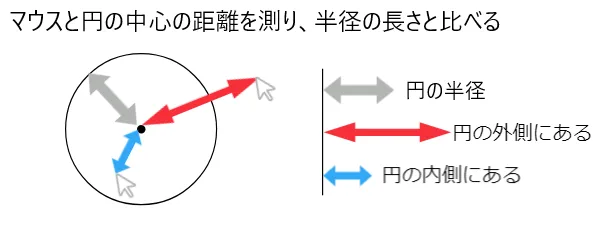
円にマウスが触れると色が白色から赤色（RGB = 255,0,0）に変わるプログラムを考えてみましょう。

プログラム中の ? にどんな比較演算子（==,<,>,=>,=<）何を入れたら良いか考えてみてね。

float x = 300;
float y = 200;


void setup(){
  size(600,400);
}


void draw(){
  background(255);


// マウスが円の内側にあるか？
  if(dist(x,y,mouseX,mouseY) ? 200/2){
    fill(255,0,0);
  }else{
    fill(255);
  }


  ellipse(x,y,200,200);
}

２．マウスと四角形の当たり判定

四角の図形にマウスが当たっているかどうかを調べるプログラムを考えてみましょう。

まず、マウスが四角の横の範囲にあるかどうか調べましょう。

(1)マウスが四角の横の範囲にあるか?

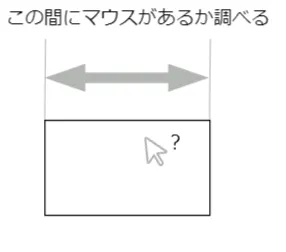
Untitled

rect(x,y,100,50) と四角を描くと、プログラム中の x が左端の座標となります。また、右端の座標は、 左端の座標＋横の大きさ なので、 ｘ+ 100 となります。　

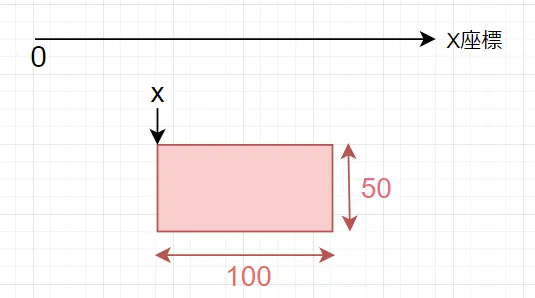
Untitled

ProcessingのX座標は右になるほど大きくなるので、 マウスのX座標が四角の左の座標 ｘ よりも大きく、なおかつ 四角の右の座標 x+100 より小さい と当たっているということになります。

2つの条件を式にするとこうなります。（ mouseXが四角の中に入っているイメージで、あえて2つの式の右辺と左辺のmouseXを入れ替えています。）

x < mouseX mouseX < x+100

2つの式が成り立つときだけ、つまり「 なおかつ 」とするには && でつなぎます。（ & はShift キー ＋ & で入力できます）この記号を論理演算子 といいます。Scratchの「かつ」と同じですね。プログラミング的な表現だと 「AND条件」（アンドじょうけん） ともいいます。

Untitled

x < mouseX && mouseX < x+100

では、マウスが四角の横の範囲にあるときだけ、四角の色が変わるプログラムで確認してみましょう。

float x = 100;
float y = 50;


void setup(){
  size(600,400);
}


void draw(){
  background(255);


// マウスが四角の横の範囲に収まっているか？
  if(x < mouseX && mouseX < x+100){
    fill(255,0,0);
  }else{
    fill(255);
  }


  rect(x,y,100,50);
}

このプログラムではまだ横の範囲しか調べていないので、マウスが四角と重なってなくても四角の色が変わってしまう場合がありますね。四角の縦の範囲も調べる必要があります。

(2)マウスが四角の縦の範囲にあるか?

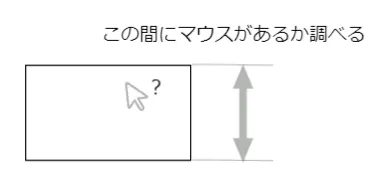
Untitled

四角の縦の範囲も、2つの座標の間にマウスがあるかどうかを調べるので、以下の式のようになります。

mouseYが四角の上の座標より下か？　&&　mouseYが四角の下の座標より上か？

rect(x,y,100,50) と四角を描くと、ProcessingのY座標は下になるほど大きくなるので、プログラム中のyが上の座標となります。また、下の座標は、 上の座標＋縦の大きさ なので、 y+50 となります。　

y < mouseY && mouseY < y+50

そして、(1)マウスが四角の横の範囲内にあるか？と(2)マウスが四角の縦の範囲内にあるか？の2つの条件が成り立っている必要があるので、さらに 2つの条件を論理演算子 && でつなげます。

(1)マウスが四角の横の範囲にあるか？ && (2)マウスが四角の縦の範囲にあるか？

やってみよう

前述の横の範囲しか調べていないプログラムを改良して、横だけでなく縦の当たり判定も追加してみよう。

３．円と円の当たり判定

円（正円）同士の当たり判定は、それぞれの円の中心間距離（dist）がそれぞれの円の半径（r1、r2）を足したものよりも短ければ、当たっていると判定することができます。

dist(x1,y1,x2,y2) < r1+r2

float x1 = 300;
float y1 = 200;
float x2 = 0;
float y2 = 200;
float r1 = 100;  //円1の半径
float r2 = 50;   //円2の半径


void setup() {
  size(600, 400);
}


void draw() {
  background(255);
  x2 += 1;
  if (dist(x1, y1, x2, y2) < r1+r2) {
    fill(255, 0, 0);
  } else {
    fill(255, 255, 255);
  }
  ellipse(x1, y1, r1*2, r1*2);
  ellipse(x2, y2, r2*2, r2*2);
}

4．円と四角形の当たり判定

ボールキャッチゲーム や ブロック崩し などでは、ボール（円）とブロック（四角形）の当たり判定になります。

これは「ボールキャッチゲームでの当たり判定」を参照してください。

5．（応用）四角形と四角形の当たり判定

四角形同士の当たり判定は、下記の判定式で求めることができます。

if ( (px < (ex+ew)) && (ex < (px+pw))
  && (py < (ey+eh)) && (ey < (py+ph)) ){
  • px, py, pw, ph ：プレーヤーのｘ座標、ｙ座標、幅、高さ
  • ex, ey, ew, eh ：敵のｘ座標、ｙ座標、幅、高さ
float px = 0;
float py = 175;
float pw = 75;
float ph = 75;
float ex = 250;
float ey = 200;
float ew = 100;
float eh = 100;


void setup() {
  size(600, 400);
}


void draw() {
  background(255);
  px += 1;
  if ( (px < (ex+ew)) && (ex < (px+pw))
    && (py < (ey+eh)) && (ey < (py+ph)) ) {
    fill(255, 0, 0);
  } else {
    fill(255, 255, 255);
  }
  rect(ex, ey, ew, eh);
  rect(px, py, pw, ph);
}

（参考） 以下はこの当たり判定の式について詳しく知りたい人のための解説です。ちょっと複雑ですが、興味がある方は挑戦してみてください。これが理解できる人は、かなり論理的な思考力の持ち主です。（行頭の>をクリック）

まず、 ｘ軸（横方向） のところだけで見てみましょう

    (px < (ex+ew)) && (ex < (px+pw))

例えば下記のようにプレーヤーと敵が当たっている場合、 (px < (ex+ew)) も (ex < (px+pw)) も真（ True ）になることを確認してください。

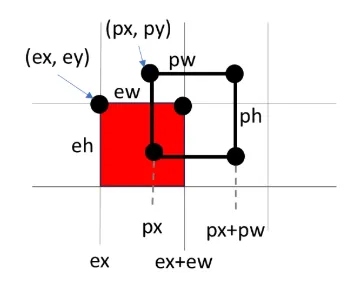
図7 当たっている場合 図7 当たっている場合

やってみよう

下記のように当たっている場合も前述の式が成り立つことを確認してください。

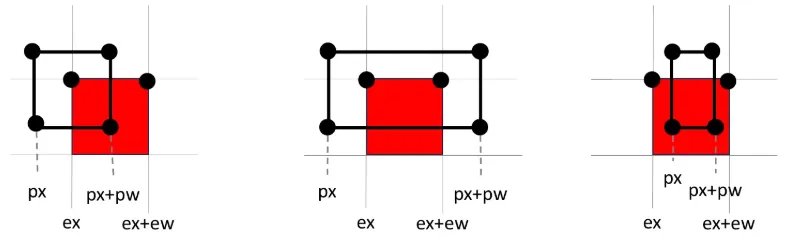
図8 その他の当たっている場合 図8 その他の当たっている場合

このような当たっていない場合は式が成り立たないことを確認してください。

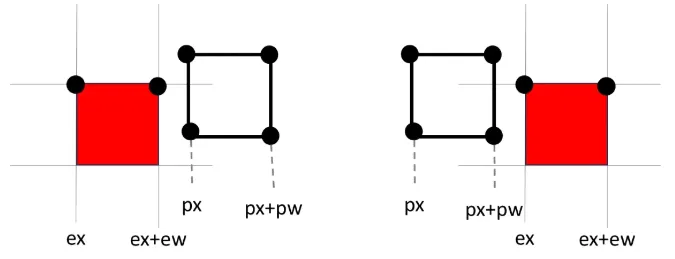
図9 当たっていない場合 図9 当たっていない場合

（参考）当たり判定式はややこしくて嫌いだ、という人へ（行頭の>をクリック）

(px < (ex+ew)) && (ex < (px+pw)) なんてややこしい！４パターンもの当たりを考えなければならないなんてめんどくさい！と思うかもしれません。でもこれ、よくよく見ると、 「当たっていない」の否定 なんです。つまり、「当たっていない」は、図９からわかるように、

px > (ex+ew) （図９の左側）　または ex > (px+pw) （図９の右側）

です。これはすぐにわかりますよね。これを式で書くとこのようになります。

(px > (ex+ew)) || (ex > (px+pw))

これが当たっていない判定の式です。これの否定は、不等号を逆にして、or（||）をand（&&）にするから、

(px < (ex+ew)) && (ex < (px+pw))

となります。（正確には=が入りますが、説明を簡単にするため省略しています）

これは 当たり判定の式 です。

（興味がある人は、前述の「当たり判定の式」ではなく「当たっていない判定の式」でプログラムを書いてみてください。場合によってはそちらの方が計算量オーダー的に優れているかもしれません。）

ｙ軸（縦方向） でも同様に考えることができます。

ｘ軸、ｙ軸の両方に関して真（当たっている）であるとき、この２つの四角は当たっている、とすることができます。

やってみよう

ｙ軸の場合の図を自分で描いて確かめてみよう

※四角形同士以外の図形の組み合わせ（他の多角形や円）や、画像の当たり判定の場合はもっと複雑になります。例えば下図のように、四角の領域同士は当たっているけど画像は当たっていない場合でも、これまでの四角形同士の当たり判定では当たったと判定されてしまいます。

興味のある方は各自ネット等で調べてみてください。内積などの知識があれば、効率的なコードを書くことができるでしょう。また、PImageクラスの様々なメソッドやプロパティも使えるかもしれません。

image.png